Maximale Flughöhe einer Drohne
Eignen sich Drohnen für die Höhenforschung oder die Aufnahme von Luftbildern aus großen Höhen? Anhand von theoretischen Betrachtungen und mit praktischen Daten des „DJI Phantom 2 Vision“ wird in diesem Fachartikel die maximal erreichbare Höhe mit einem Quadrocopter untersucht. Mit der maximalen Reichweite beschäftigt sich dieser Fachartikel. Abschließend werden Optimierungsmöglichkeiten aufgezeigt um mit einem Copter in große Höhen aufsteigen zu können. Die Kernfrage lautet dabei, wie viele Höhenmeter kann ein Quadrocopter steigen?
Diesen Artikel können Sie hier downloaden.
Bitte beachten Sie die entsprechenden Vorschriften (z.B. die Aufstiegsgenehmigung). Alle Angaben ohne Gewähr und unter Ausschluss jeglicher Haftung.

Foto: Dirk Brunner; Lizenz: CC BY SA 3.0
Beispiel-Drohne
Um die Idee des Höhenflugs mit einer Drohne (oder Modellhelikopter) zu bewerten sind Eckdaten aus der Praxis erforderlich, mit denen schrittweise weitergearbeitet wird. Dieser Fachartikel ist, soweit möglich, leicht verständlich geschrieben. Hintergrundwissen und weitere Informationen finden Sie im Anhang.
Durchführung Höhenflug
Die Drohne wird bei dem Höhenflug autark arbeiten. Mittels GPS steigt er senkrecht über der Startposition so weit wie möglich nach oben bis der Akku nahezu leer ist. Danach erfolgt ein kontrollierter Sturzflug, bei dem die Rotoren für eine stabile Fluglage entsprechend gebremst werden. Dies funktioniert nur bei Motoren mit geringem Rastmoment. Energierückgewinnung ist möglich. Kurz vor dem Boden wird das Modell abgefangen und sicher gelandet. So weit die Theorie.Technisch limitierende Faktoren bei einem solchen Höhenflug sind:
- Abnahme der Luftdichte mit steigender Höhe. Propeller müssen schneller drehen und die maximale Drehzahl der Propeller (bzw. Motor/Regler) wird erreicht
- Akkukapazität
- Umgebungstemperatur
- Gesamter Wirkungsgrad des Modells
- Gewicht
Luftdruck und Propellerdrehzahl
Der Luftdruck nimmt mit der Höhe ab, weshalb die Drehzahl der Propeller, bei gleichem Schub, erhöht werden muss (siehe Herleitung 1 im Anhang).Je höher das Flugmodell steigt, umso schneller müssen sich die Propeller drehen. Dies bedeutet, dass ein Propeller, der sich auf Meereshöhe mit 8000 Umdrehungen pro Minute dreht, in 2000 Metern Höhe über NHN (Normalhöhennull, Höhe über dem Meeresspiegel) mit 9120 U/min drehen muss um den gleichen Standschub zu erzeugen (einfache Betrachtung ohne Temperatureinfluss). Die Drehzahl des Propellers kann nicht beliebig gesteigert werden, da ansonsten der Propeller beschädigt wird. Motor und Regler besitzen ebenfalls eine maximale Drehzahl. Aus dem Diagramm 1 ist der Zusammenhang zwischen Propellerdrehzahl und Luftdruck ersichtlich. Eckdaten von Höhenflug tauglichen Drohnen in Tabelle 1.
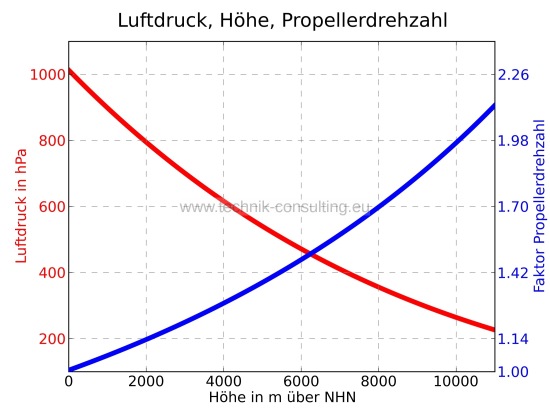
Foto: Dirk Brunner; Lizenz: CC BY SA 3.0
Diagramm 1 - Luftdruck, Höhe, Propellerdrehzahl
| Wert | Beispieldrohne | DJI Phantom 2 Vision |
|---|---|---|
| Schubeffizienz ?Schub | 4 g/W | 4 g/W |
| Abfluggewicht m | 2,5 kg | 1,16 kg |
| Antrieb Eingangsleistung | 4 x 600 W | 4 x 140 W |
| Akkutechnologie | LiPo | LiPo |
| Zellenzahl | 6S (22,2 V) | 3S (11,1 V) |
| Akkukapazität | 4,9 Ah | 5,2 Ah |
| Energieinhalt Akku | 391 kJ | 208 kJ |
| Akkugewicht | 750 g | 367 g |
| cw-Wert | 0,9 | 0,9 |
| Strömungswirksame Fläche A | 0,04 m2 | 0.026 m2 |
| Systemwirkungsgrad ?System | 30% | 30% |
Tabelle 1 - Höhenflugtaugliche Drohnen
Optimale Steigrate
Folgende Überlegung lässt vermuten, dass es eine optimale Steigrate (Steiggeschwindigkeit) für den Copter gibt:- Im Schwebeflug wird Akkuenergie nicht in Höhe umgesetzt.
- Bei einem sehr schnellem Steigflug nimmt der Luftwiderstand mit der Steiggeschwindigkeit quadratisch stark zu, wodurch viel Energie zur Überwindung des Luftwiderstands benötigt wird. Die Leistung nimmt dabei mit der dritten Potenz zu!
Um die Frage der optimalen Steigrate beantworten zu können ist es notwendig eine Drohne mathematisch / physikalisch näher zu betrachten.
Schubkraft Propeller
Die Schubkraft die ein Propeller erzeugt lässt sich mit folgender Formel ermitteln: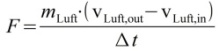
Wirkungsgrad der Steigleistung
Der Wirkungsgrad für die Steigleistung wird bestimmt mit:
Je größer ?Steigleistung ist, um so effizienter wird die (Akku-) Energie in Höhe umgesetzt. Der Zusammenhang zwischen Wirkungsgrad, Steiggeschwindigkeit und Höhe ist bei unserer Beispiel-Drohne aus Diagramm 2 abzulesen.
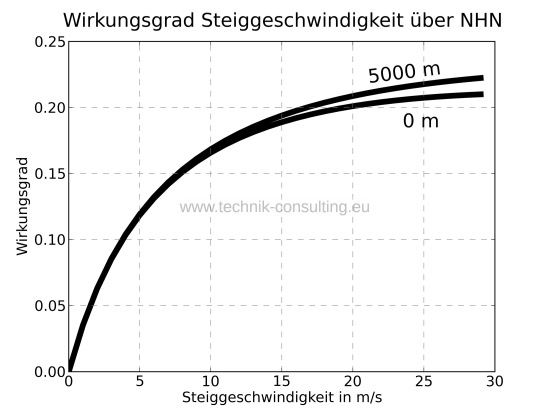
Foto: Dirk Brunner; Lizenz: CC BY SA 3.0
Diagramm 2 - Wirkungsgrad Steiggeschwindigkeit über NHN
Mit steigender Höhe nimmt der Luftwiderstand ab, da die Luftdichte geringer wird. Der Luftwiderstand fällt dadurch weniger ins Gewicht, weshalb mit steigender Höhe der Wirkungsgrad zunimmt. Aus dem Diagramm 2 ist ersichtlich, dass bei geringen Steiggeschwindigkeiten der Wirkungsgrad stark nachlässt. Beim Schweben (Steiggeschwindigkeit = 0 m/s) ist der Wirkungsgrad der Steigleistung erwartungsgemäß null, da keine Höhe gewonnen wird.
Die optimale Steiggeschwindigkeit
Mit Hilfe der Mathematik lässt sich die optimale Steiggeschwindigkeit aus ?Steigleistung in Abhängigkeit der Höhe berechnen. Siehe hierzu Diagramm 3.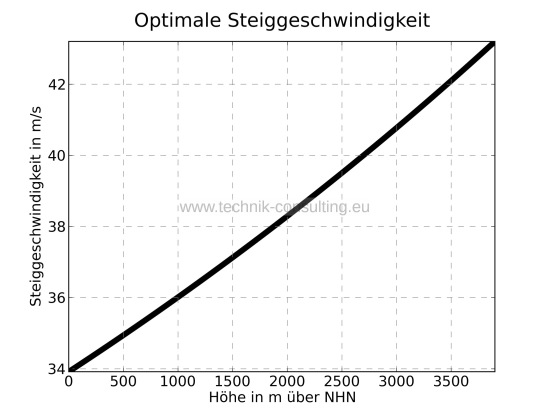
Foto: Dirk Brunner; Lizenz: CC BY SA 3.0
Diagramm 3 - Optimale Steiggeschwindigkeit
Die Steigrate, um im optimalen Wirkungsgrad zu bleiben, ist enorm. Auf Meereshöhe wäre dies bei unserem Beispielcopter eine vertikale Steiggeschwindigkeit von 120 km/h. Beim „DJI Phantom 2 Vision“ sind es immerhin gut 100 km/h. Laut Hersteller schafft das Modell maximal 22 km/h vertikale Steiggeschwindigkeit. Somit kann das Modell nicht mit optimalem Wirkungsgrad steigen.
Benötigte Motorleistung für die optimale Steiggeschwindigkeit
Die benötigte Motorenleistung für den Beispiel-Copter, um die optimale Steigrate zu halten, ist in Abhängigkeit der Höhe aus Diagramm 4 ersichtlich.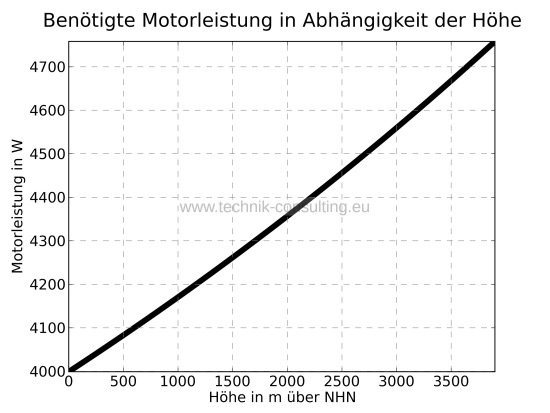
Foto: Dirk Brunner; Lizenz: CC BY SA 3.0
Diagramm 4 - Benötigte Motorleistung in Abhängigkeit der Höhe
Unsere Beispiel-Drohne hat maximal 2400 W Motoreingangsleistung. Dies genügt nicht, um einen Steigflug mit optimalem Wirkungsgrad zu ermöglichen. Der Wirkungsgrad bricht jedoch erst bei geringen Steigraten deutlich ein. Mit 2400 W schafft unser Modell in Abhängigkeit der Höhe die Steigraten im Diagramm 5.
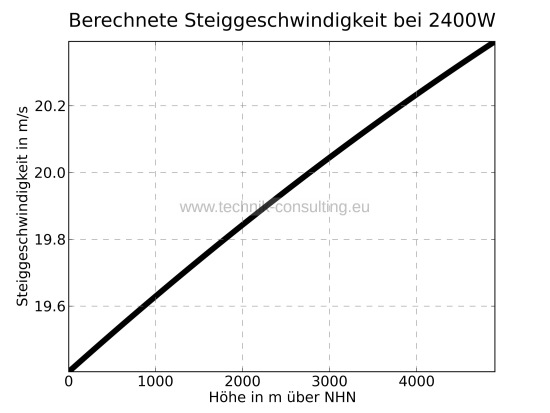
Foto: Dirk Brunner; Lizenz: CC BY SA 3.0
Diagramm 5 - Steiggeschwindigkeit Beispielcopter 2400 Watt
Das Modell bewegt sich mit 2400 W Motoreingangsleistung nicht im optimalen Steigratenbereich von 34 m/s auf Meereshöhe, sondern erreicht 19 m/s auf Meereshöhe. Der Wirkungsgrad, die Akkuenergie in Höhe umzuwandeln, sinkt dadurch von etwa 22% auf ca. 20%.
Der „DJI Phantom 2 Vision“ hat maximal 560 W Motoreingangsleistung. Die berechnete Steigleistung auf Meereshöhe liegt (Diagramm 6) mit dieser Motorisierung bei ca. 6,8 m/s. Optimal wären 29 m/s. Der Wirkungsgrad des „DJI Phantom 2 Vision“ sinkt damit von etwa 19% auf ca. 13%.
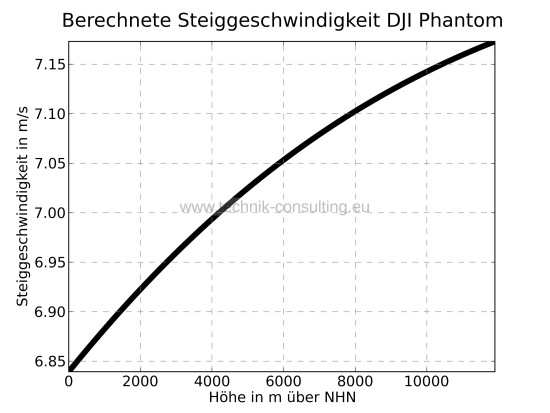
Foto: Dirk Brunner; Lizenz: CC BY SA 3.0
Diagramm 6 - Steiggeschwindigkeit DJI Phantom 2 Vision
Ausströmgeschwindigkeiten am Propeller
Die maximale (Steig-) Geschwindigkeit ist begrenzt durch die Kombination von Propellersteigung und Drehzahl. Dadurch ergeben sich entsprechende Ausströmgeschwindigkeiten am Propeller wie aus Diagramm 7 ersichtlich.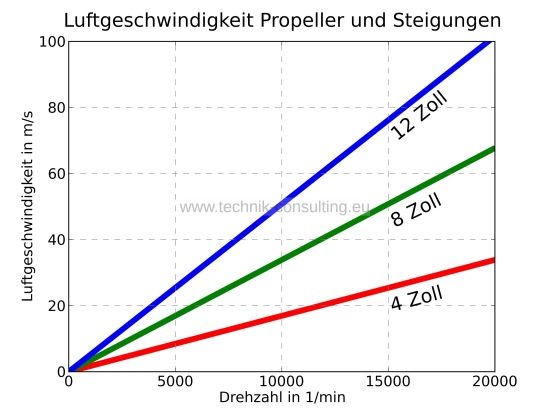
Foto: Dirk Brunner; Lizenz: CC BY SA 3.0
Diagramm 7 - Luftgeschwindigkeiten am Propeller
In der Realität ist die Luftgeschwindigkeit aufgrund von Strömungsverlusten ca. 10% geringer als angegeben. Der vom Propeller erzeugte Luftstrom muss deutlich schneller sein, als die Aufstiegsgeschwindigkeit von gut 70 km/h (19 m/s). Die Steigung des Propellers sollte demnach mindestens 8 Zoll bei einer Drehzahl von etwa 8000 1/min betragen.
Maximale Steighöhe
Der Energiegehalt des Akkus von dem Beispielcopter beträgt 390 kJ und der des „DJI Phantom 2 Vision“ 208 kJ. Da das Modell für den Sinkflug sowie das Abfangen in Bodennähe weitere Energie benötigt, stehen für den Steigflug etwa 350 kJ bzw. 180 kJ zur Verfügung. Wenn bei dem Sinkflug über die Propeller Energie zurückgewonnen wird, kann noch mehr Akkuenergie für den Aufstieg verwendet werden.Die Beispiel Drohne kann damit von Meereshöhe etwa auf 2800 m Höhe aufsteigen (Diagramm 8) und beispielsweise Luftaufnahmen anfertigen. Der „DJI Phantom 2 Vision“ schafft 2300 m Höhe (Diagramm 9).
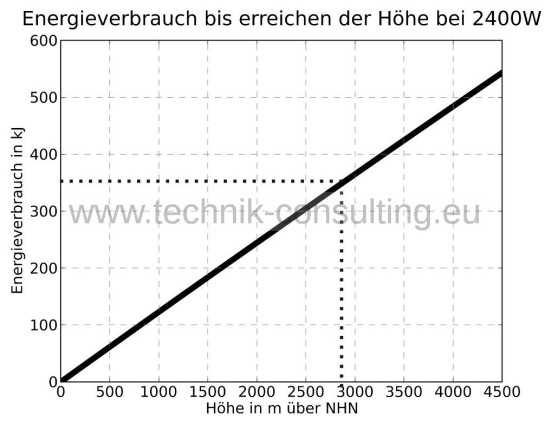
Foto: Dirk Brunner; Lizenz: CC BY SA 3.0
Diagramm 8 - Energieverbrauch Steigen Beispielcopter 2400 Watt
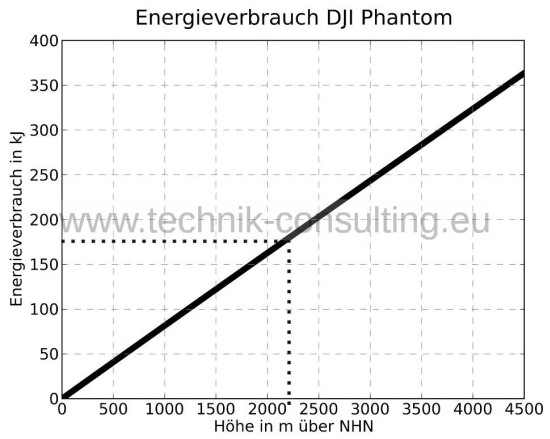
Foto: Dirk Brunner; Lizenz: CC BY SA 3.0
Diagramm 9 - Energieverbrauch Steigen beim DJI Phantom 2 Vision
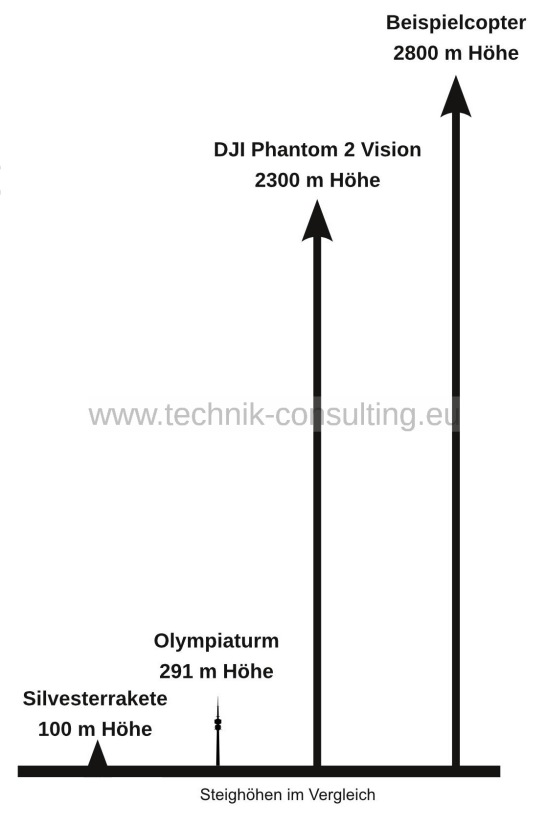
Foto: Dirk Brunner; Lizenz: CC BY SA 3.0
Größenvergleich
Zeitdauer für den Aufstieg
Um in diese Höhe vorzudringen werden etwa 140 Sekunden (Diagramm 10) bzw. 320 Sekunden (Diagramm 11) beim „DJI Phantom 2 Vision“ benötigt. Danach ist der Akku fast leer.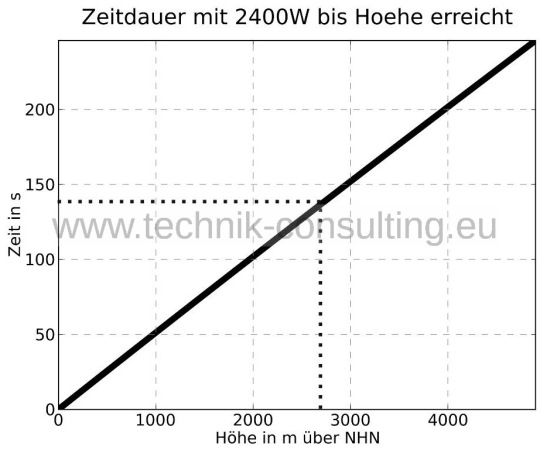
Foto: Dirk Brunner; Lizenz: CC BY SA 3.0
Diagramm 10 - Zeitdauer Beispielcopter 2400 W
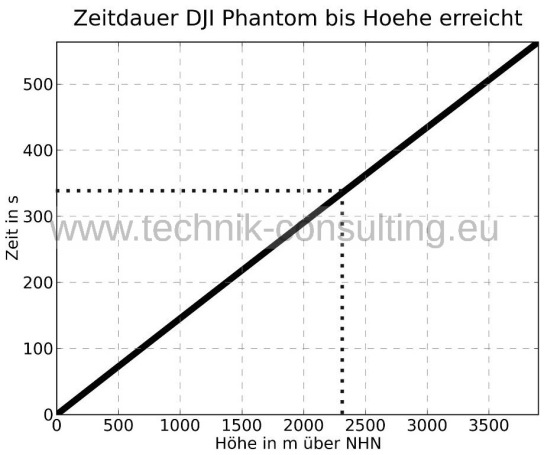
Foto: Dirk Brunner; Lizenz: CC BY SA 3.0
Diagramm 11 - Zeitdauer beim DJI Phantom 2 Vision
Flugdaten der Drohne
Daten des Fluges mit dem Beispielcopter und „DJI Phantom 2 Vision“ sind in Tabelle 2 angegeben.| Wert | Beispielcopter | DJI Phantom 2 Vision |
|---|---|---|
| Maximale Höhe über NHN in m | 2800 | 2300 |
| Benötigte Zeit für den Aufstieg in s | 150 | 310 |
| Elektrische Leistungsaufnahme in W | 2200 | 540 |
| Akkuenergieinhalt bei maximaler Höhe | 10% | 10% |
| Gesamtstromaufnahme im Steigflug in A | 100 | 50 |
Tabelle 2 - Flugdaten der Drohne
| Wert | Max. Höhe über NHN in m | Höhengewinn in m |
|---|---|---|
| Beispielcopter | 2800 | 0 |
| Beispielcopter 10% leichter | 3200 | +400 |
| Beispielcopter 10% besserer cw-Wert | 2900 | +100 |
| Beispielcopter 10% besserer ?Schub | 3000 | +200 |
| Beispielcopter 10% besserer ?System | 3100 | +300 |
| Beispielcopter 10% geringere Fläche | 2900 | +100 |
| Stark optimierter Copter | 4700 | +1900 |
Tabelle 3 - Optimierung Drohne
Optimierte Drohne
Die technischen Daten eines optimierten Quadrocopters sehen Sie in Tabelle 4. Dieser Copter schafft eine Höhe von 4700 m über NHN.
Foto: Dirk Brunner; Lizenz: CC BY SA 3.0
Schnelle Drohne
| Wert | Optimierter Copter |
|---|---|
| Schubeffizienz ?Schub | 5 g/W bzw. 0,05 N/W |
| Abfluggewicht (mit Nutzlast) m | 2,0 kg |
| Antrieb Dauereingangsleistung | 4 x 600 W |
| Akkutechnologie | LiPo |
| Zellenzahl | 6s (22,2 V) |
| Akkukapazität | 4,9 Ah |
| Energieinhalt Akku | 391 kJ (94 kcal) |
| Akkugewicht | 750 g |
| cw-Wert | 0,5 |
| Strömungswirksame Fläche A | 0,04 m2 |
| Systemwirkungsgrad ?System | 35% |
| Maximale Höhe | 4700 m über NHN |
Tabelle 4 - Optimierte Drohne
Fazit
Mit der Beispiel-Drohne sind maximale Flughöhen von über 2000 m Höhe möglich. In dieser Höhe lassen sich bereits eindrucksvolle Luftaufnahmen anfertigen. Speziell ausgelegte Drohnen schaffen fast 5000 m Höhe. Solche Flugmodelle können in Zukunft vielfältig eingesetzt werden für- Die einfache und kostengünstige Erforschung der untersten Troposphäre.
- Kartographie und Luftaufnahmen
- Transport im Gebirge (z.B. Medikamente oder Notrationen für Bergsteiger in Not)
Welche weiteren Einsätze möglich sind, wird die Zukunft zeigen.

Für Fragen zur Durchführung, Optimierung oder Berechnung von Höhenflügen stehe ich Ihnen gerne zur Verfügung.
| Symbol | Einheit | Bedeutung |
|---|---|---|
| a | ° | Anstellwinkel des Propellers gemessen bei etwa 0,7 x Radius |
| ?Schub | 1 | Wirkungsgrad der Schuberzeugung |
| ?System | 1 | Wirkungsgrad des gesamten Modells, mit dem die Akkuenergie in Höhe umgewandelt wird. |
| p | 1 | Kreiszahl |
| ? | kg/m3 | Luftdichte |
| ?t | s | Zeitintervall |
| A | m2 | Strömungswirksame Fläche des Modells |
| cw | 1 | Strömungswiderstandskoeffizient (cw-Wert) |
| D | m | Durchmesser der Luftschraube |
| Ekin,Luft | J | Kinetische Energie der Luft |
| F | N | Schubkraft bzw. Kraft |
| h | m | Höhe |
| m | kg | Abfluggewicht (mit Nutzlast) bzw. Masse |
| mLuft | kg | Luftmasse |
| n | 1/s | Drehzahl des Propellers |
| p(h) | Pa | Luftdruck in Abhängigkeit der Höhe |
| P | W | Elektrische Leistung |
| S | m | Steigung des Propellers |
| vLuft | m/s | Geschwindigkeit der durch die Luftschraube beschleunigten Luftmasse |
| vsteigen | m/s | Steiggeschwindigkeit des Modells senkrecht nach oben |
| vtangential | m/s | Tangentialgeschwindigkeit des Propelles gemessen bei etwa 0,7 x Radius |
Tabelle 5 - Legende
Herleitungen
Herleitung 1 - Herleitung der Drehzahländerung mit der Höhe im Schwebeflug
Internationale Höhenformel
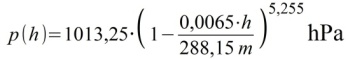
Impulserhaltungssatz
Ausströmgeschwindigkeit
Kraft für den Schwebeflug
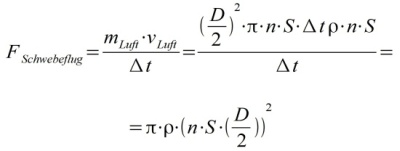
Die Kraft F soll in der Höhe konstant sein, woraus folgt:
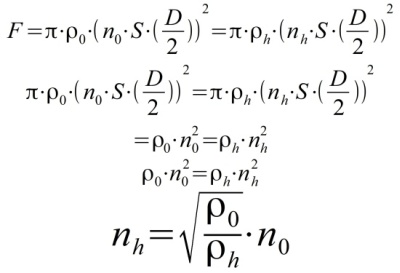
Herleitung 2 - Schubeffizienz und Systemwirkungsgrad im Schwebeflug
Berechnung Systemwirkungsgrad aus praktischen Messwerten im Schwebeflug: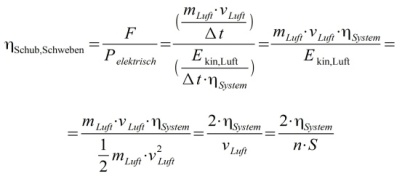

?Schub=0,08 N/W; n =8.000 1/min (133 1/s); S=4,5“ (0,11 m)? ?System = 58%. Dieser Wert beschreibt, wie effizient die Akkuenergie in Bewegungsenergie der Luft umgesetzt wird. Dies ist eine vereinfachte Betrachtung, da v über den Propellerradius gesehen nicht konstant, sowie n mal v nicht der realen Ausströmgeschwindigkeit entspricht. Bei näherer Betrachtung des Propellerwirkungsgrades im Steigflug ist beim „DJI Phantom 2 Vision“ von einem ?System = 30% auszugehen und von einem ?Schub=0,04 N/W für den Steigflug.
Herleitung 3 - Wirkungsgrad Steiggeschwindigkeit
Die Gesamtleistung des Modells ist:Benötigte elektrische Leistung für den Schwebeflug
Benötigte elektrische Leistung um den Luftwiderstand zu überwinden. Stellen Sie sich einen schwebenden Copter vor, bei dem der Luftwiderstand durch ein Gewicht simuliert wird. Die zusätzlich benötigte Leistung ist PLuftwiderstand,steigen.
Benötigte elektrische Leistung um das Modell zu heben. Stellen Sie sich einen schwebenden Copter vor, der sich selbst an einem Seil langsam in die Höhe zieht.
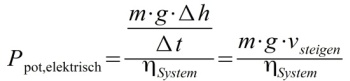
Damit lässt sich eine Gleichung für den Systemwirkungsgrad aufstellen.

Herleitung von ?Schub siehe Herleitung 2.
Herleitung 4 - Schubeffizienz und Systemwirkungsgrad im Flug
Die vom Propeller erzeugte Kraft ist: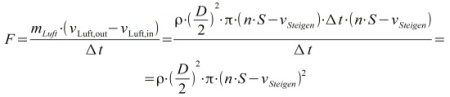
Mit der beschleunigten Luftmasse
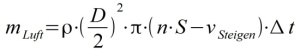
Impuls des Propellers
Kinetische Energie der Luftmasse
Wirkungsgrad der Schuberzeugung
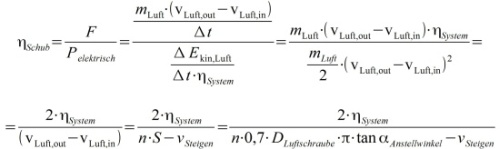
Achtung: Diese Formel gilt nur, wenn vLuft,out >> vLuft,in, da:
- Propellerdurchmesser begrenzt
- System aus dem Standschub bestimmt wurde.
- System ändert sich mit vLuft,in
Der Systemwirkungsgrad ist weiterhin abhängig von Anstellwinkel, Drehzahl etc. .
Weitere Formeln
Ausströmgeschwindigkeit am Propeller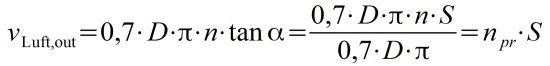
Impuls der Luftmasse
Anstellwinkel Luftschraube:
Winkelmessung des Anstellwinkels bei ca. 0,7 bis 0,75 mal Radius.


Für Fragen zur Durchführung, Optimierung oder Berechnung von Höhenflügen stehe ich Ihnen gerne zur Verfügung.
Diesen Artikel können Sie hier downloaden.